Anomoly Dectection 顾名思义“异常识别”，给定一个 dataset（with features），训练出一种模型，当出现新数据时，判断该数据是否正常。
首先我们先来简单聊下高斯分布 Gaussian Distribution（正态分布 Normal Distribution），我们认为中间状态是事物的常态，过高和过低都属于少数。高斯分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。高斯分布的概率密度函数为：
所以识别异常值的过程就变为求解概率的数学问题，当概率值低于某个阈值 ϵ ，即 p(x) < ϵ 时，我们把它认为是异常值。
Anomoly Dectection Original Model
Algorithm
应用于实际例子中，给定训练集 {x1, … ,xm}，其中每个 x 是一个 n 维向量（n 个 features）。那么 x 为正常值的概率为每一个单独特征为正常值的概率的乘积：
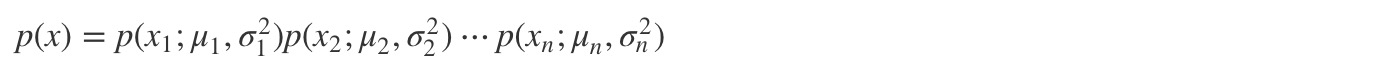
Features Transform
在异常识别中，feature 是一个算法好坏的重要因素，但是有些 feature 的分布不满足高斯分布，这时我们就需要进行 features transform.
检查转换完的 feature 是否满足高斯分布图
Developing and Evaluating an Anomaly Detection System
之前我们讨论概率密度函数时，没有用到 y 值，即把所有的 training data 当作 unlabled data 来用。但是如何评估算法的好坏呢？
- 标记数据，区分中正常数据和异常数据
- 将数据集按 60(training) : 20(cv)：20(test) 来拆分，其中 training data 全部为正常数据，而将异常数据平均分配到 cv & test 中
- 用全部为正常数据的 training data 来求解 μ 和 σ2
Anomaly Detection vs. Supervised Learning
经过上面的描述，是不是有一种感觉，Anomaly Detection 和 Supervised Learning 中的分类问题很像？的确是这样的，两者的目的一样，但应用场景不同： Use anomaly detection when…
- We have a very small number of positive examples (y=1 … 0-20 examples is common) and a large number of negative (y=0) examples.
- We have many different “types” of anomalies and it is hard for any algorithm to learn from positive examples what the anomalies look like; future anomalies may look nothing like any of the anomalous examples we’ve seen so far.
Use supervised learning when…
- We have a large number of both positive and negative examples. In other words, the training set is more evenly divided into classes.
- We have enough positive examples for the algorithm to get a sense of what new positives examples look like. The future positive examples are likely similar to the ones in the training set.
Multivariate Gaussian Distribution
之前提到的异常识别算法在某种情况下会出错，如：
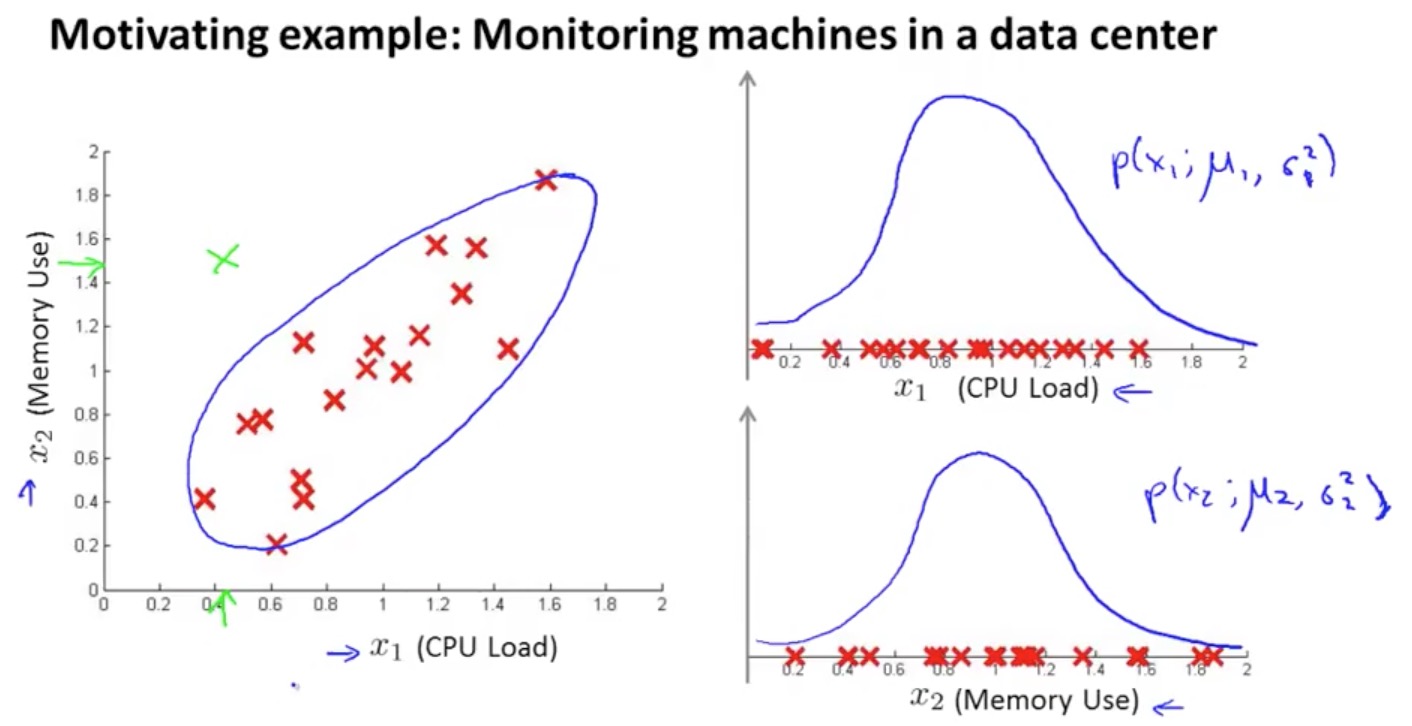图中用绿色标记出来的数据是一个异常数据（离别的正常数据很远），但是它的两个 features 分布都在正常范围内，通过之前讨论的算法是无法捕捉这种情况的：即 features 之间有相互关系，本图中的两个特征是一同递增／递减。
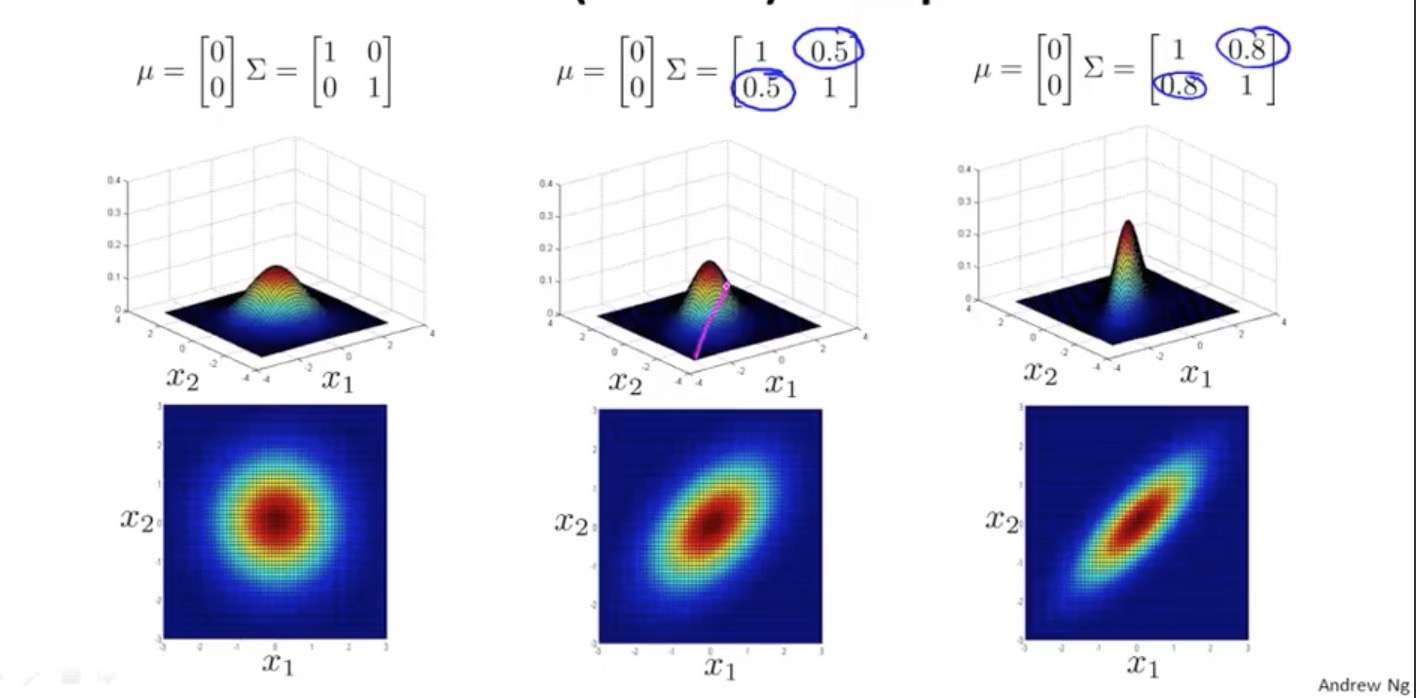
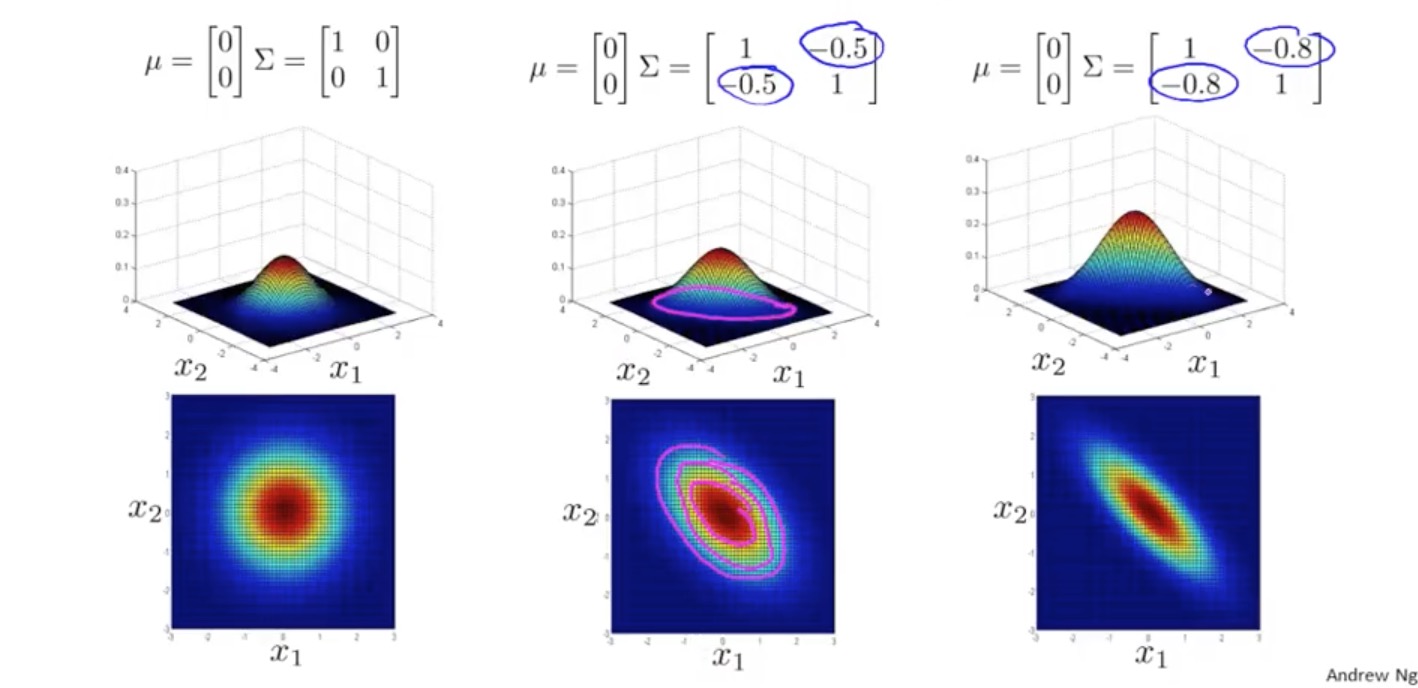
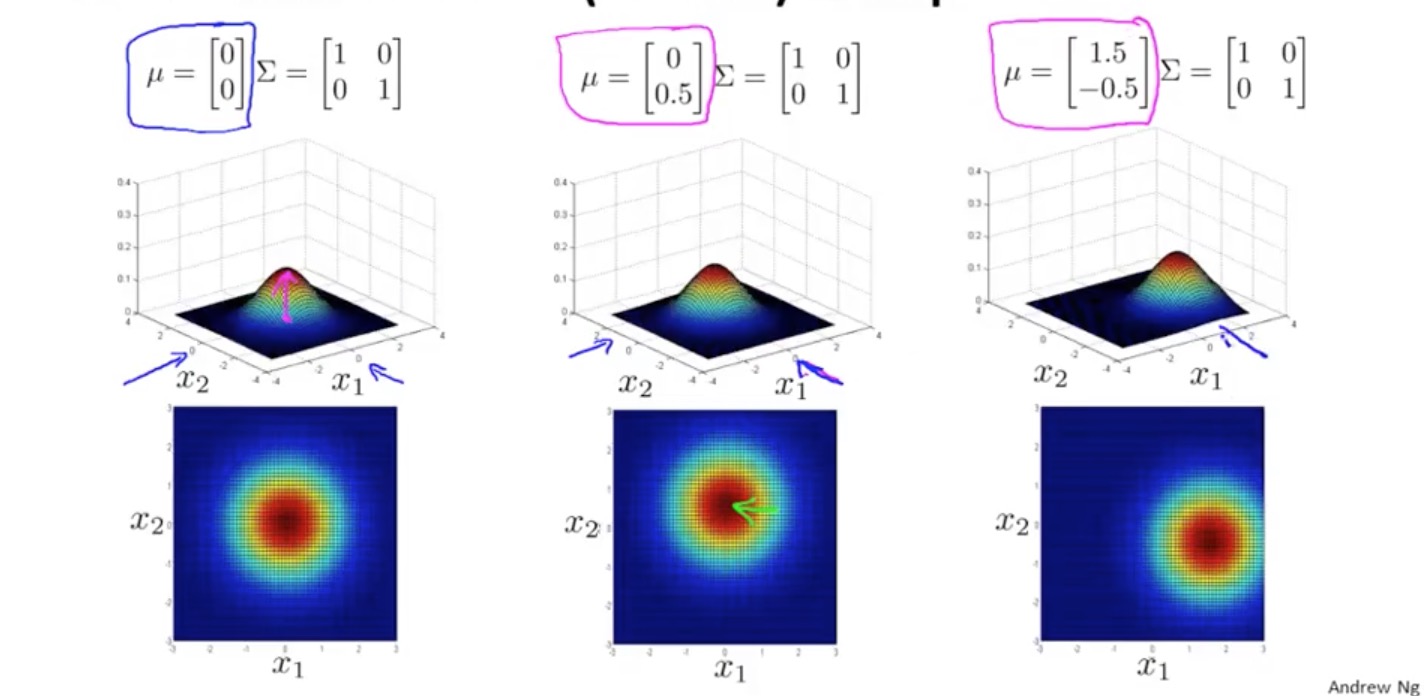
所以我们引入了一种优化算法：Multivariate Gaussian Distribution（多元高斯分布）。这种算法不是把 n 维 features 独立计算概率值再相乘，而是把所有特征当成一个整体，可以自动捕捉到不同 features 之间的关系，并用一个统一的公式计算：
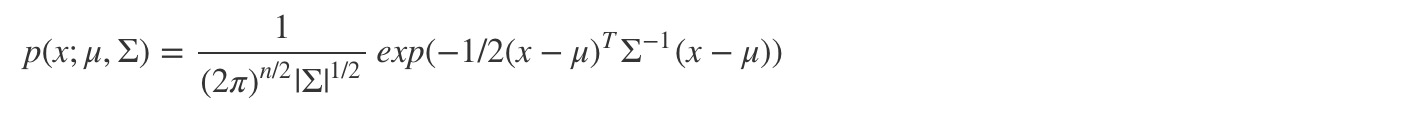
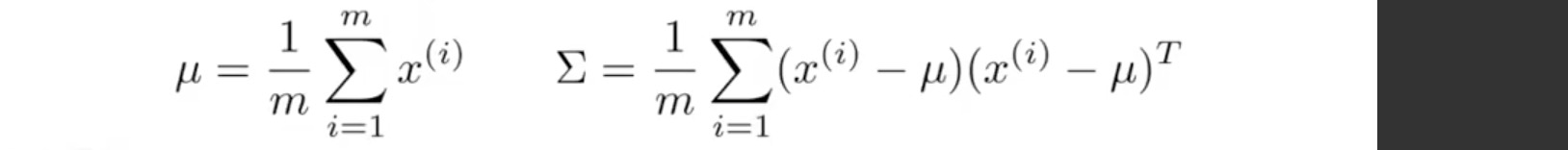其中，μ ∈ ℝn , Σ ∈ ℝn×n
该公式的等高热度图为：
Make a Choose between Original Model and Multivariate Gaussian Distribution
原始模型可以当做多元高斯分布的一个特例，即特征之间没有相互关联，反应到数学公式上：Σ 是一个对角矩阵（即除对角线外，矩阵的其他元素全部为 0）。
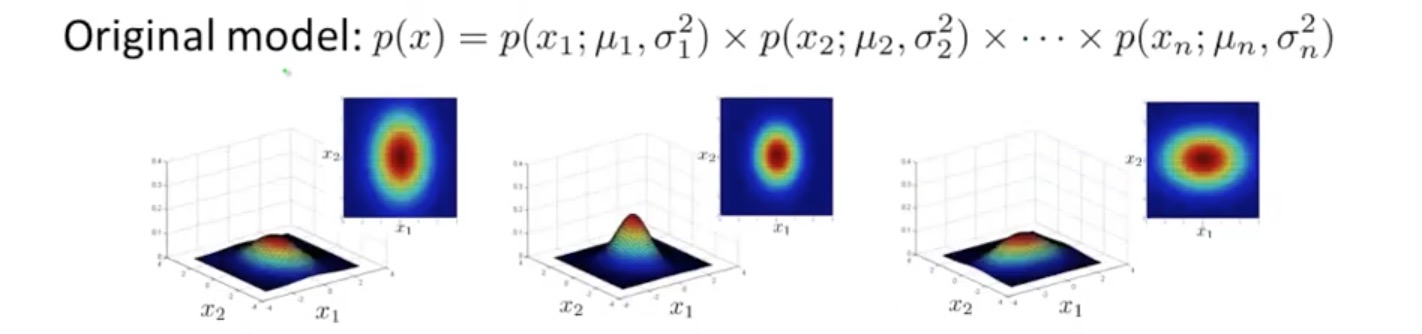
其实为了解决原始模型无法顾及 features 间关联的问题，可以通过添加 feature 来解决。之前我们提到，计算机的 CPU load 和 memory 本质上有正相关性，虽然单独计算两个 features 无法体现出相关性来，但是我们可以添加 x3 = CPU load / memory 这个新 feature 来反映这种关联性。
由于算法复杂度的原因，不同的场景可以选择不同的算法来执行：
| original model | Multivariate Gaussian Distribution |
|---|---|
| 需要手动创建 feature 捕获特征关系 | 自动捕捉特征关联关系 |
| 计算速度更快 | 计算速度慢 |
| 适合 training data 比较小的情况 | 适合 training data 远远大于 features 的情况 |