之前我们已经介绍了逻辑回归、神经网络等机器学习算法，今天来聊聊另一种非常常用的算法：Support Vector Machine（支持向量机）。
首先我们来回顾下逻辑回归问题。对于逻辑回归，预测函数如下，当z » 0时，h(x)≈1，当 z « 0时，h(x) ≈ 0.
对于单个 example 的 cost function 如下：
SVM
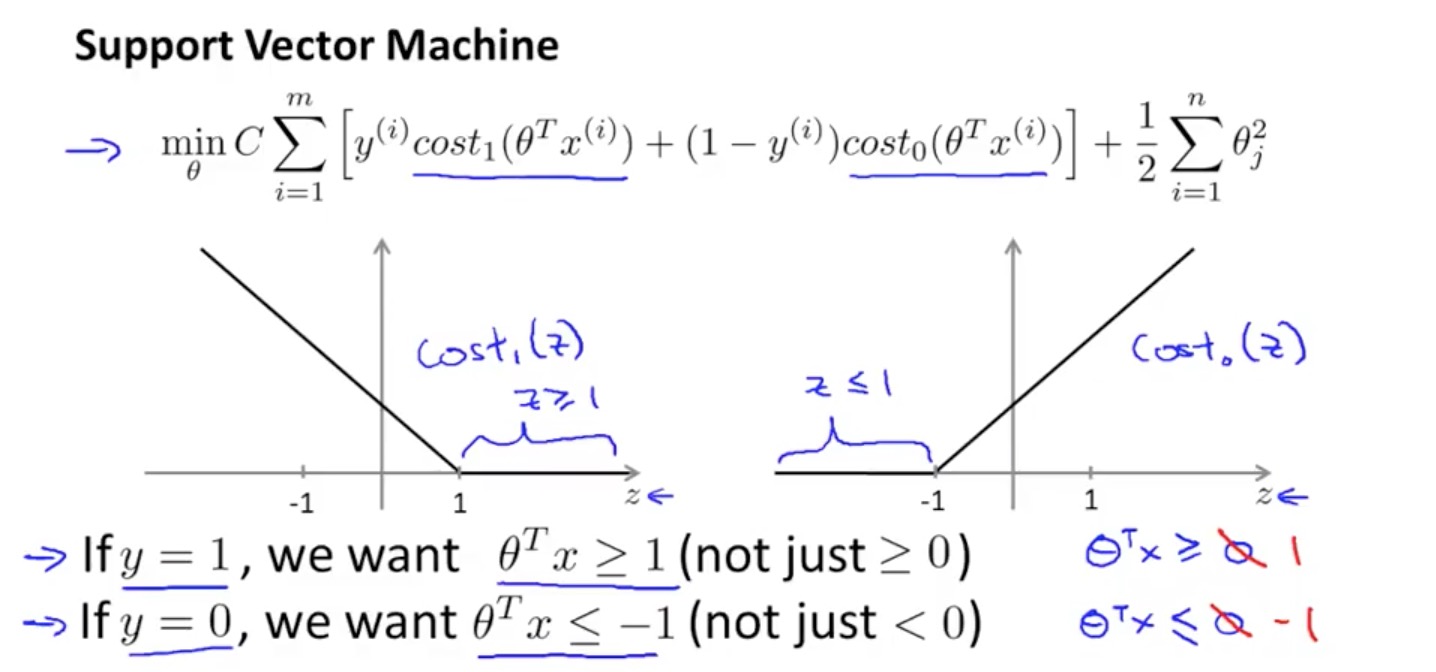
SVM 算法与普通逻辑回归算法的不同在于 cost function 的定义，cost function 不再是一条曲线，而是变成了直线。对于 y = 1 时的 cost function，当θ’x ≥ 1 时，cost function 为0，θ’x ≤ 1时，我们用一条直线替代原先的曲线，同理对于 y = 0时的 cost function，当θ’x ≤ -1时，cost function 为0，否则是一条直线。
逻辑回归算法的 cost function
SVM 算法的 cost function
需要注意：
- 由于 m （example count）是常量，所以在 SVM 中习惯删掉
- SVM 中单个 example 的 cost function 为 cost1、cost2，即前面提到的两条相交的直线
- SVM 中 C = 1 / λ
Large Margin Classifier
有些人习惯将 SVM 称作 Large Margin Classifier（大间距分类器），为什么这么说呢，因为在普通的逻辑回归算法中，当 y ＝ 1 时，我们仅仅要求 θ’X ≥ 0，当 y ＝ 0 时，要求 θ’X ≤ 0。但是 SVM 要求θ’X ≥ 1 ／θ’X ≤ －1，即更大程度的区分度：
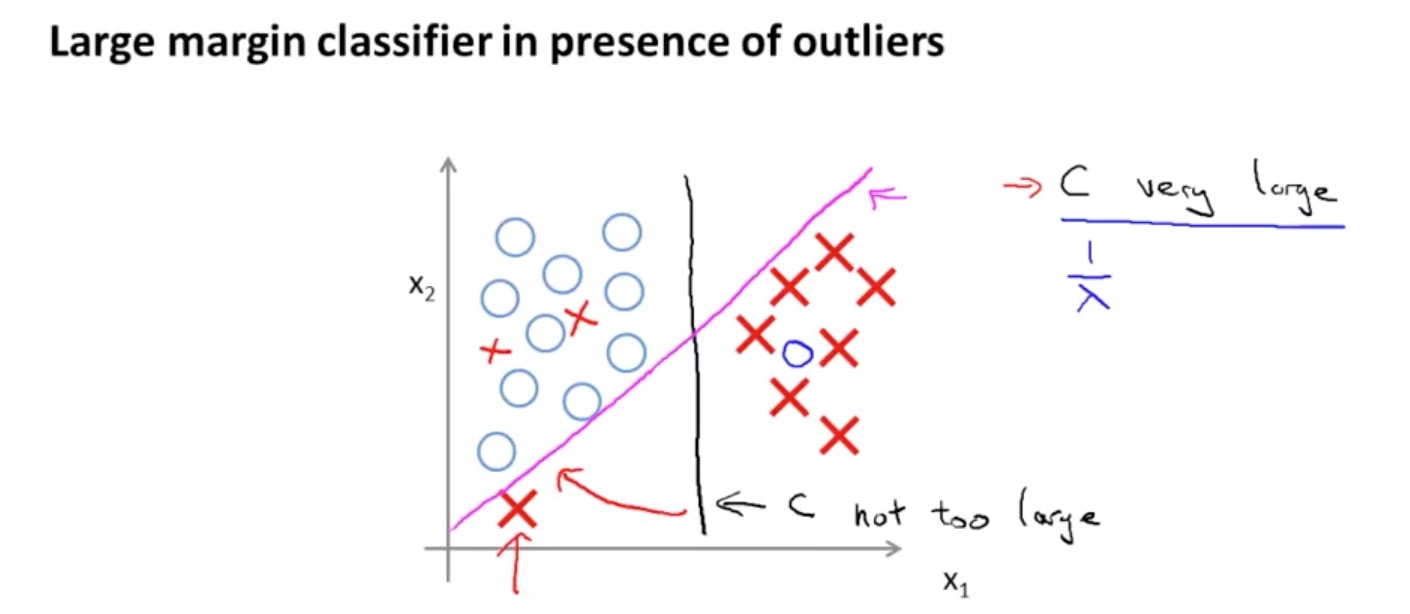
这里的 C 是个关键因子，考虑如下图所示，如果数据集中出现一个异常点，当 C 设置很大时(λ 很小)，会发生 overfit 现象，所以我们需要谨慎的设置 C：
Mathematics Behind Large Margin Classification
在数学上，两个向量的内积公式如下：u’v = v’u = p⋅||u|| = u1⋅v1 + u2⋅v2。其中 p = length of projection of v onto the vector u。需要记住：If the angle between the lines for v and u is greater than 90 degrees, then the projection p will be negative.
现在再来看 SVM 的 cost function：
最右侧的正则化公式可以变形为：
为了降低 cost function 的值，左侧的公式可变形为：
我们反过来看，为了降低 full cost function，右侧的正则化参数不能太大，即 Θ 不能太大，θ 较小，但是 p . ||Θ|| 又需要大，则 p 只能较大，即 X 映射到 Θ 上的长度较大，所以 decision boundaries 只能尽可能的远离正负样本集，这也正式 SVM 叫做 Large Margin Classifier 的原因。
Kernels
核函数可以让我们训练一些基于 SVM 的复杂的、非线性的分类器。那么什么是核函数呢？核函数本质是相似度函数，即度量两个向量的相似度，使用的比较多的一个核函数是 Gaussian Kernel(高斯核函数):
可以看出，当 x ≈ l 时，f ≈ 1。当 x 远离 l 时，f ≈ 0。
那么 kernel 如何与 SVM 结合呢？
首先我们回顾下 SVM 的 cost function:
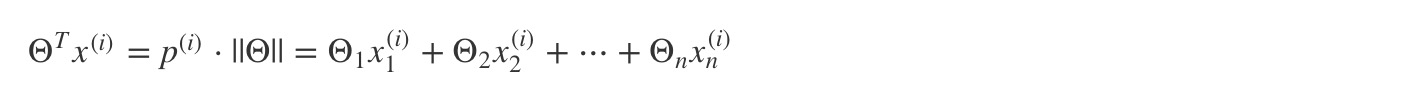这里我们不再使用 Θ’ * X，而是使用 Θ’ * f，f 值是一个 m 维 vector，表明 x 与当前的 m 个训练样本集的 similarity， 具体如下：
所以，融合 SVM & Kernel 后的 cost function 如下：
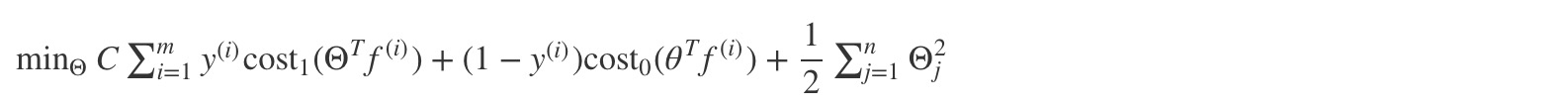
当然，kernel 不仅可以和 SVM 算法结合，也可以和 logistic regression 算法结合，不过由于 SVM 在cost function 上做的优化，所以 kernel & SVM 运行的效率更高，也更常用。
SVM & Kernels parameters optimize
SVM 中涉及到参数 C 的选择，kernel 涉及到 σ2的选择：
Multi-class classification 大部分的 SVM packages 已经内置了 multi-class classification function。如果要自己实现，原理其实跟之前提过的类似，如果有 K 种输出，需要训练 K 个 SVM，即训练出 K 个 Θ.
Logistic regression vs SVMs vs Neural Network
ML 算法的选择主要考虑两个点，m(number of training examples) & n(number of features)
- If n is large (relative to m), then use logistic regression, or SVM without a kernel (the “linear kernel”)
- If n is small and m is intermediate, then use SVM with a Gaussian Kernel
- If n is small and m is large, then manually create/add more features, then use logistic regression or SVM without a kernel.
总结：
- Neural Network 适用于上述所有场景，但是 Neural Network 有自己的缺点：训练速度慢
- logistic regression 与 SVM without a kernel 的适用场景是一致的。以及当 m 较大时，SVM with a kernel 性能会很差
- 但是，对于大多数情况来说，核心的问题仍然在于你有多少 data，多少 features
参考资料
https://www.coursera.org/learn/machine-learning/resources/Es9Qo