上期从总体上聊了下 neural network，本篇 post 将深化学习 neural network。重点聊聊神经网络的 cost function 以及一种高效的算法：back propagation。
neural network cost function
当 neural network 的 output layer 有k (>2)个输出值时，h(x) 不再是一个 real number，而是一个 k 维向量，对应的 cost function 如下：
注意：theta本身包含 theta0, 在正则化表达式中的 theta 应去除 theta0。
back propagation
现在我们有了 cost function，接下来需要求解 cost function 的导数，今天介绍一种新方法：back propagation。
在介绍 back propagation 前，先来介绍一个新的概念 delta: “error” of node j in layer。对于输出层来说，delta ＝ a - y. (a: h(x), y: actual output)
所谓向后传播，即在求解 delta 时，先求解最后一层（输出层）的 delta，然后以此 back propagation 求解每一层的 delta:
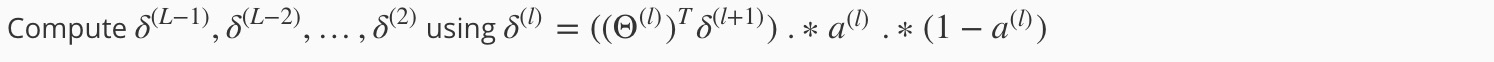需要注意，这里最后的公式其实是 g(z) 对 z 的偏导数：
back propgation algorithm
最后将各个模块组合后的 cost function 对theta 的导数如下图：
详情可参考：course by Andrew Ng
gradient checking
由于 back propagation 非常复杂，为了在求解的过程中检验代码的正确性，提出了一种 gradient checking （梯度检验）的方法。
梯度检验的原理在于，(theta + epsilon) 与(theta - epsilon) 在 y 函数上的连线的斜率近似于函数在 theta 处的导数。
用代码来表示：
但是由于求解 gradient checking 非常的慢，所以一般在开始运行 back propagation 时，测试 back propagation 的输出与 gradient checking 的输出是否近似，判断无误后，表明 back propagation 已经在正确运行，其实应该停掉 gradient checking，只运行 back propagation，保证效率。
putting it together
至于如何选择 hidden layer 的层数以及每层的 unit 数，遵循以下建议：
- theta 的初始值，一般来说，有两种选择。
1：选取[-ε, ε], ε = 0.12 * 0.12；
2：
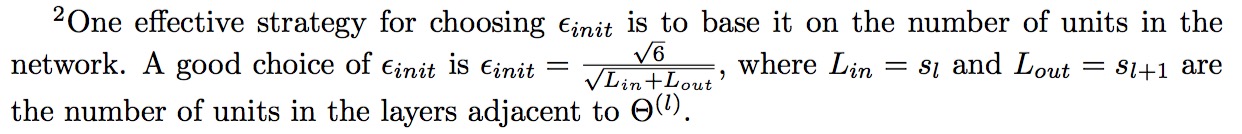
- 默认使用单个 hidden layer
- 如果使用多个 hidden layer 的话，一般每层的 unit 数保持一致
- 一般来说，unit 越多越好（当然计算量越大）
- 一般来说，unit 取稍大于 input feature 的个数
可以看出，所谓的 back propagation，本质就是给定初始的 theta ，求解 cost function 偏导数的值。之后利用梯度下降算法（或者更高级的 BFGS算法等），让 theta 朝正确的方向移动（cost function 随着 iterator 递减），直至找出 local optima。