最近在学习 Machine Learning 的知识，一些听 Andrew Ng 的 coursera 课，一边做习题，即使这样，仍感觉听完就糊涂，学完就忘，so，重新捡起中断了一年多的 blog。前期的关于 Linear Problem 的内容我争取尽早补上吧。本周主要介绍 Classification Problem 以及 Logistic Regression（逻辑回归）的知识。
Classification Problem
有监督学习分为两类问题：regression problem（回归问题）& classification problem（分类问题）。上周聊过了 regression problem，这周来总结下 classification problem。
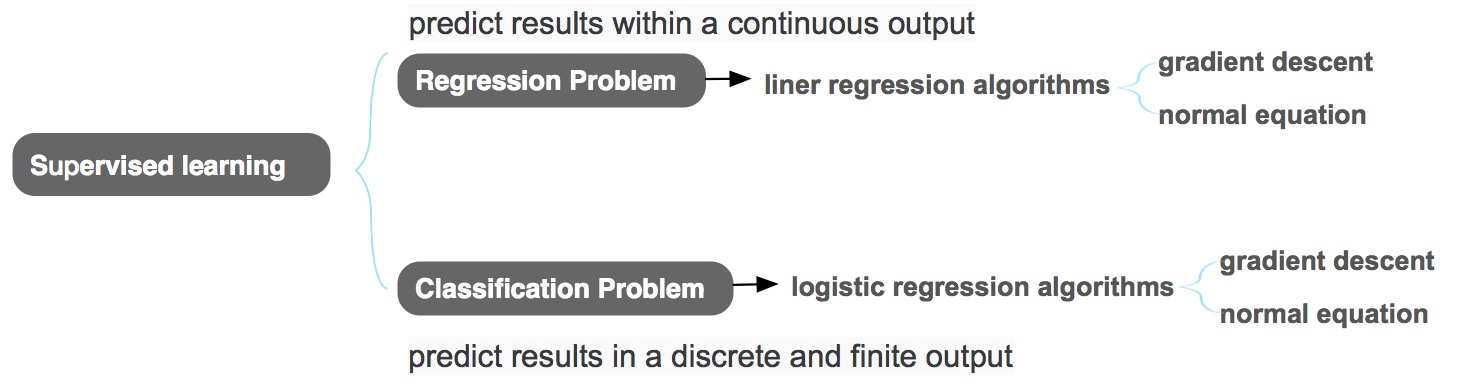
所谓 Classification Problem（分类问题），与Regression Problem的不同是，它的output是有限个数的、离散的值,这里的有限个数不局限在｛0，1｝两个值，是可数范围内的多个，如：
- email 是否为垃圾邮件
- 肿瘤是良性／恶性
Logistic Regression
Classification Problem 不可以用 Linear Regression（线性回归算法）来解决，需要用 Logistic Regression（逻辑回归算法，名称中的regression是由于历史原因导致的，请无视）。
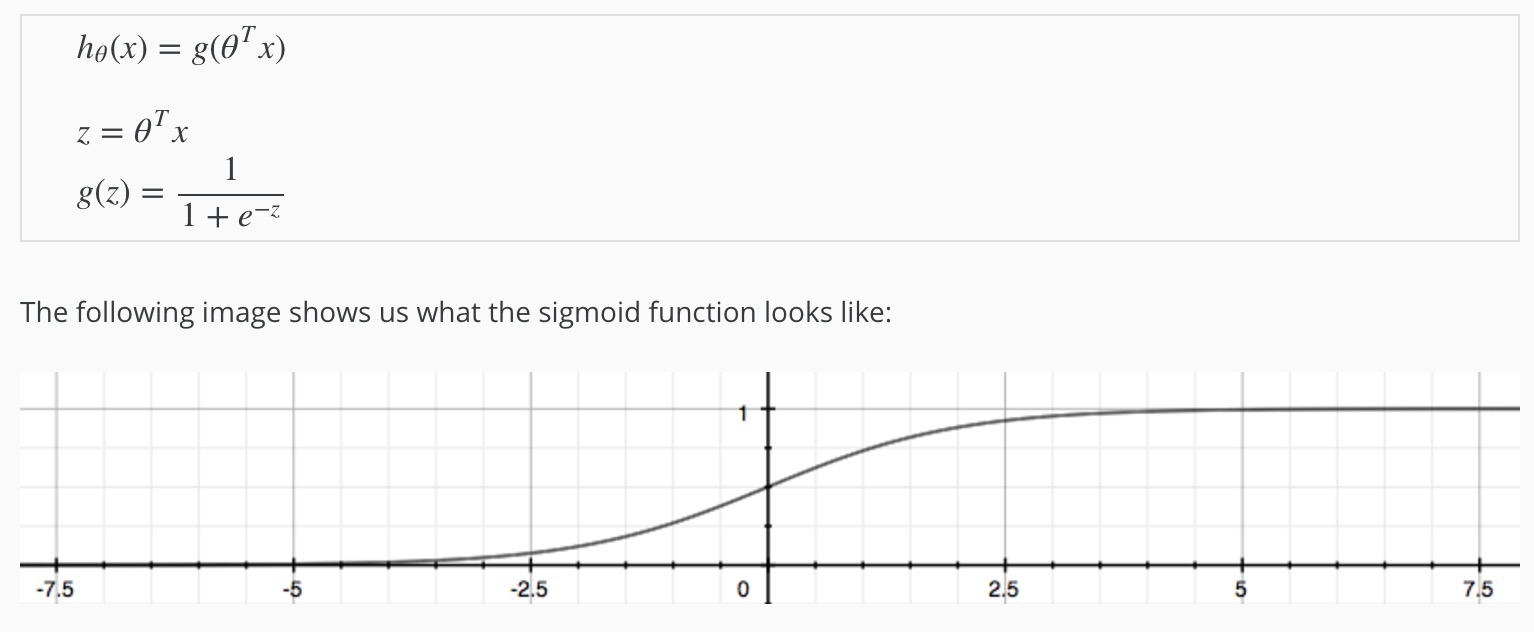
逻辑函数（Logistic function）也叫 S 型函数（Sigmoid function）。
当输出值是2个时，h(x)的的输出表示结果为1的可能性，当h(x) >= 0.5,则预测y = 1，否则y ＝ 0：
输出值是多个时：
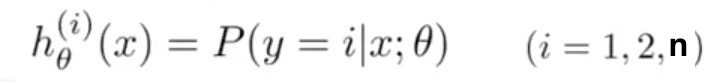
Decision Boundary
先着重介绍两个输出值的情况。可以看到，当θ’ * X = 0时（即h(x) = 0.5），这条线被称为Decision Boundary（决策边界），用于区分y = 0 & y = 1：
Overfitting
我们先通过一个线性回归的例子讨论下 overfitting 的定义及解决方案。下图中从左到右分别表示underfitting(欠拟合／高偏差) & fitting(拟合) & overfitting(过度拟合)。
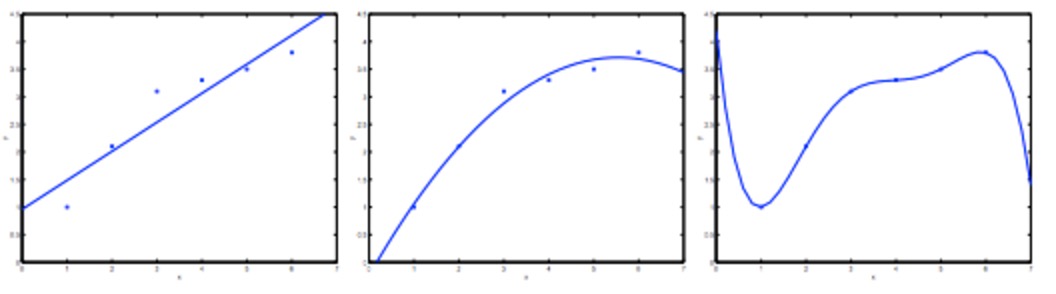过度拟合：预测模型 h(x) 过度匹配 training data，导致曲线十分扭曲，当预测新数据时，效果很差。一般来说，features过多 / 多项式的次数过大，都可能造成 overfitting。
通常来说，解决过度拟合有两种方法：
- 减少特征数量
- 人工选择features
- 通过model selection algorithm自动选择
- Regularization(正则化)
- 保留所有的features，但是减小θ值
- regularization 在线性回归问题和逻辑回归问题上都可以运用
Linear Regression 的正则化成本函数和梯度递减算法
cost function
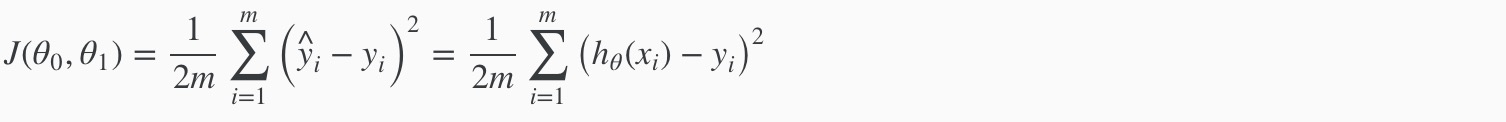
cost function for linear regression cost function
Regularization 后的cost function为下图，为了让cost function接近0，必须得降低θ1 ~ θn的值，最终达到减少overfitting的目的:
其中 λ 称为 regularization parameter，该参数既不能过大（导致underfitting），也不能过小（overfitting），具体如何选择，之后我们在介绍。
gradient descent for regularized linear regression
由于θ0不需要处罚，所以对它进行特殊处理，其中 alpha 为学习速率参数：
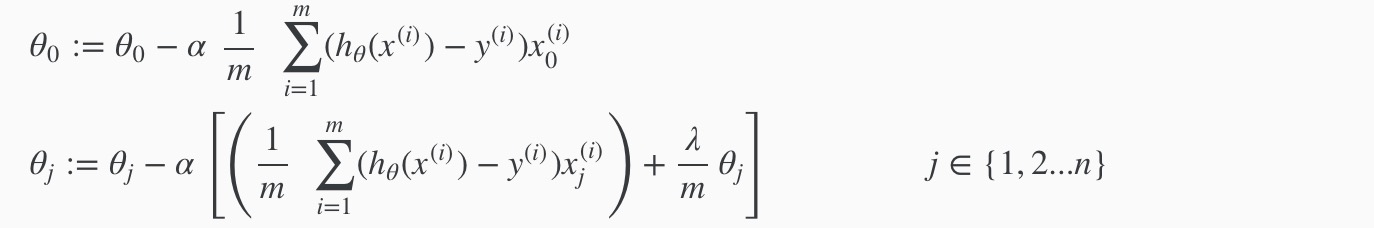
normal equation for linear regression cost function
Logistic Regression 的正则化成本函数和梯度递减算法
cost function
当逻辑回归套用线性回归的cost function时，cost function会呈现出波浪形的形状，存在大量的local optima。为解决这个问题，逻辑回归对cost function做了调整。
单个training data的cost function为：
单个training data的cost function合并后为下图：
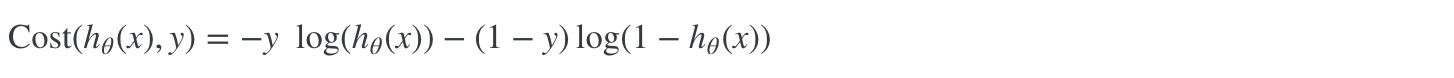
总的cost function如下图：
gradient descent
使用梯度递减求解逻辑回归的 cost function 最小值的做法和线性回归的一样，皆为：
由于梯度递减在某些情况下速度较慢，一些”Conjugate gradient”, “BFGS”, and “L-BFGS” 能更快速的求解出θ值
cost function for regularized logistic regression
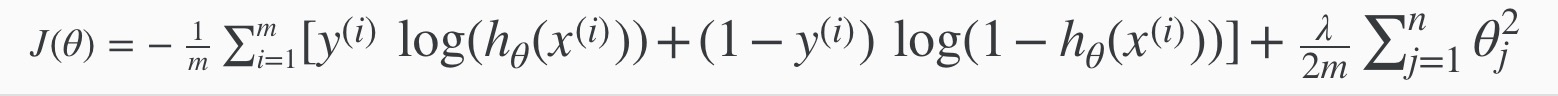同样的，用于 regularization 的项不包含 θ0.
gradient descent for regularized logistic regression
