现状
传统意义上的企业级搜索是通过像 Lucence 以及基于它而开发的 Solr / Elasticsearch 来实现的。目前我们的搜索功能已经从 Solr 迁移到 Elasticsearch。Elasticsearch 内部有几种不同的算法来评估相关度(relevance):TF-IDF、BM25、BM25F等。
但是这种模型 f(q,d) 其实是简单的概率模型,评估 query 在 doc 中出现的位置、次数、频率等因素,但是不能有效的根据用户反馈(点击/停留时间)来持续优化搜索结果。
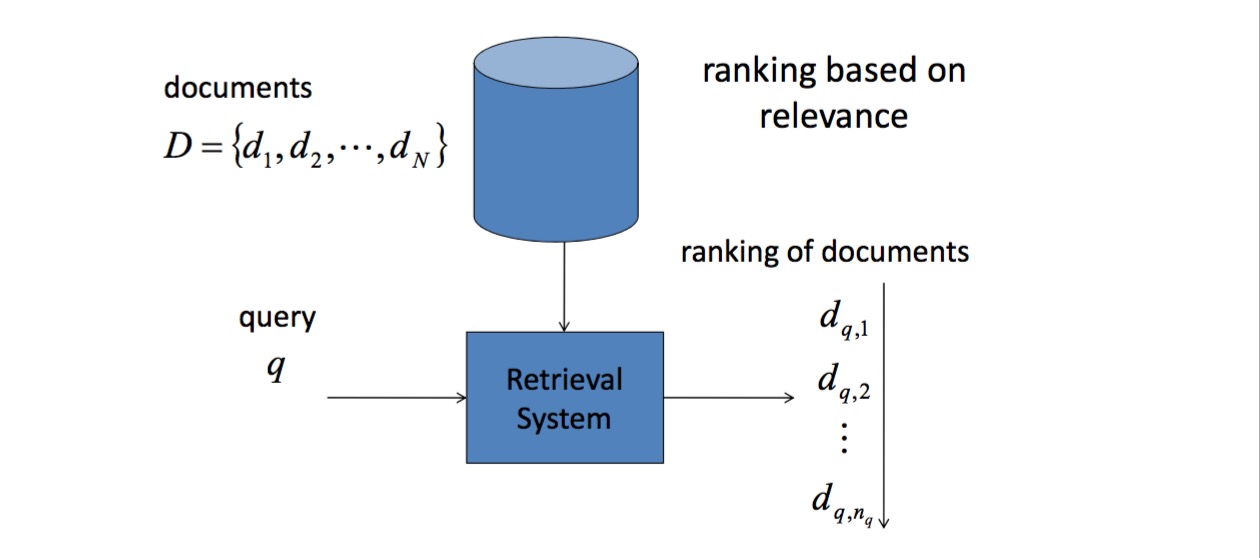
所以我们自然而然的想到使用机器学习来优化搜索排序。

Learning to rank
Learning to rank 可以应用在非常多的领域,包括 Information Retrieval (IR), Natural Language Processing (NLP), and Data Mining (DM) 等。
Learning to rank 主流分三大种方案:
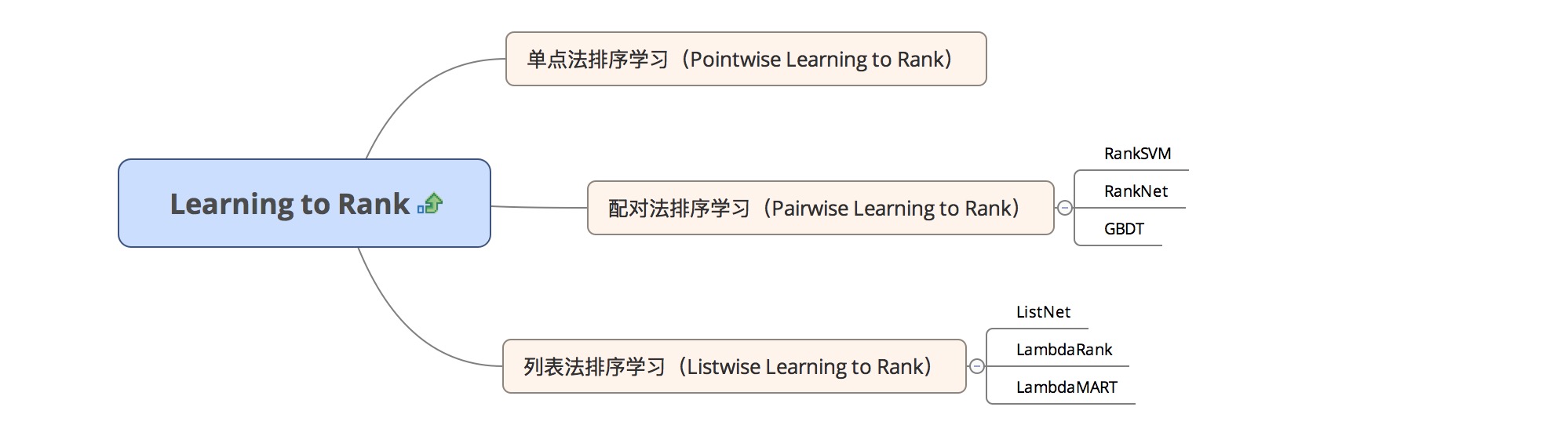
We aim to train a (local) ranking model f (q, d) = f(x) that can assign a score to a given query docu- ment pair q and d, or equivalently to a given feature vector x.
根据现有论文(包括微软亚研院)的测试数据,listwise 比 pairwise 效果更好,nDCG 值更高
Training and Testing
Learning to rank 本质上是监督学习任务,因此需要训练数据。训练数据来自用户行为产生的 query-doc pair。具体来说: qi = {q1,q2,···,qm} 是 m 个查询训练数据,qi 是第 i 个 query。
Di = {di,1,···,di,j,···,di,ni} 是 qi 对应的共 n 个 doc 结果列表。
xi,j = φ(qi,di,j) 即为特征向量。
yi = {yi,1,···,yi,j,···,yi,ni} 是 qi 对应的 n 个 doc 的分数,为标记结果。
我们的目标是根据特征向量,训练出一个 f (q, d) 模型,来预测 query-doc 的 score.
Data Labeling
有两种方式来创建训练数据,一种是人工打标签,另一种是根据 log 数据。当然,人工打标签无法做到快速、大规模化,很多时候我们采用根据用户型为日志的方式来为数据打标签。
Evaluation
- NDCG
- MAP(Mean average precision)
- Precision@n
- ERR@n
Pointwise Learning to Rank
在Pointwise方法中隐含了这样一个假设:绝对相关度假设,它假设相关度是查询无关的,即query-independent。也就是说,只要(query, document)的相关度相同,比如都为“perfect”,那么它们就被放在同一个类别里,即属于同一类的实例,而无论query是什么。然而实际上,相关度并非查询无关的。对于非常常见的查询和它的一个不相关文档,它们之间的tf可能会比一个非常稀有的查询和它的一个相关文档之间的tf更高。这样就会导致训练数据不一致,难以取得好的效果。同时,对于预测为同一类别的文档,也无法作出排序。
Pairwise Learning to Rank
相比于Pointwise方法,Pairwise方法不再对相关度作独立假设 之所以被称为文档对方法,是因为这种机器学习方法的训练过程和训练目标,是判断任意两个文档组成的文档对<D0C1,D0C2>是否满足顺序关系,即判断是否D0C1应该排在DOC2的前面。图3展示了一个训练实例:査询Q1对应的搜索结果列表如何转换为文档对的形式,因为从人工标注的相关性得分可以看出,D0C2得分最高,D0C3次之,D0C1得分最低,于是我们可以按照得分大小顺序关系得到3个如图3所示的文档对,将每个文档对的文档转换为特征向量后,就形成了一个具体的训练实例。
在配对法中,排序问题被转换成了配对分类问题/回归问题。对于分类问题,自然想到用 SVM 来做,业界主流的一种算法是 Ranking SVM。
以Ranking SVM为例,它优化的目标是使得正负样本之间的Margin最大,而并非以排序性能为优化目标。
x = {xi, xj},特征向量为一个特征组。 y ∈ {+1, −1} 标记了哪个特征应该被排前面。
RankNet
RankNet算法训练得到的排序模型是模型参数的可微函数,他可以将输入向量映射到一个实数上去,对于两个URL对儿的得分通过一个概率函数进行融合,并在该概率函数的基础上,构造交叉熵损失函数,对应的函数如下所示:
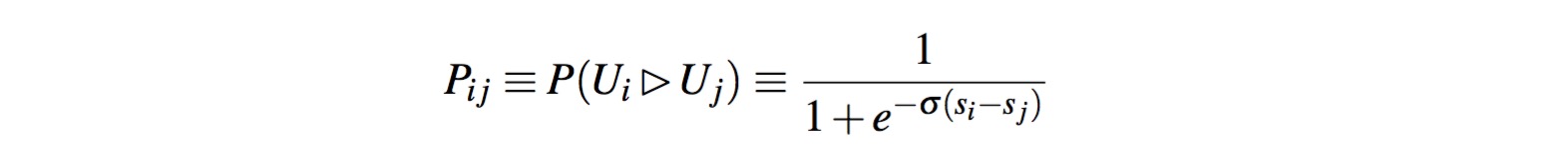
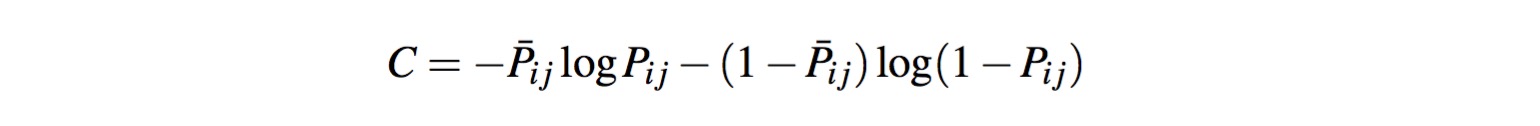
将上面两个公式结合可以得到一个更加直接的损失函数公式,如下:
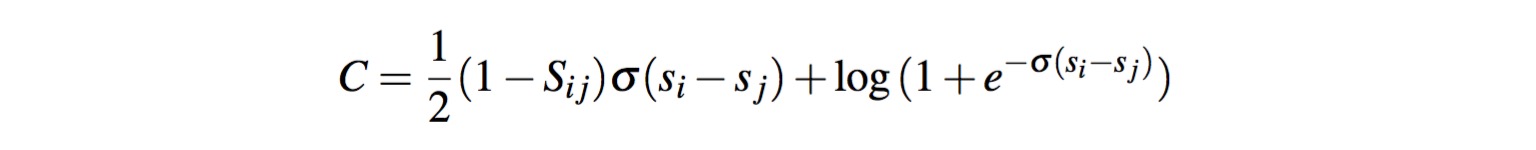
损失函数是模型参数的可微函数,自然想到用梯度下降来求解最优值。
GBDT
Pairwise 存在的问题
- pairwise 只考虑了两个文档对的相对先后顺序(最小化 document pairs 的分类误差),却没有考虑文档出现在搜索列表中的位置(最小化整体文档排序的误差)
- 根据 query 的不同,document pairs 的个数会差别很大。假设query1对应的相关文档集大小为5,query2的相关文档集大小为1000,那么从后者构造的训练样本数远远大于前者,从而使得分类器对相关文档集小的query所产生的训练实例区分不好,甚至视若无睹
Listwise Learning to Rank
单文档方法将训练集里每一个文档当做一个训练实例,文档对方法将同一个査询的搜索结果里任意两个文档对作为一个训练实例,文档列表方法与上述两种表示方式不同,是将每一个查询对应的所有搜索结果列表整体作为一个训练实例,这也是为何称之为文档列表方法的原因。
Listwise方法相比于前两种(Pointwise,Pairwise)而言,不再将 Ranking 问题直接形式化为一个分类或者回归问题,而是直接对文档的排序结果(list)进行优化。目前主要有两种优化方法:
- 直接针对Ranking评价指标进行优化。比如常用的MAP, NDCG。这个想法非常自然,但是往往难以实现,因为NDCG这样的评价指标通常是非平滑(连续)的,而通用的目标函数优化方法针对的都是连续函数。
- 优化损失函数
ListNet(Z. Cao, T. Qin, T. Liu, et al. ICML 2007)使用正确排序与预测排序的排列概率分布之间的KL距离(交叉熵)作为损失函数
LambdaRank
LambdaMART
该方法将排序问题转换为二类分类问题,利用Boosting算法优化学习目标函数。其最大特点是不显示地定义损失函数,而定义损失函数的梯度函数,以解决排序损失函数不易优化的问题。
LambdaMART is the boosted tree version of LambdaRank, which is based on RankNet.
LambdaMART is a tree ensemble based model. Each tree of the ensemble is a weighted regression tree and the final predicted score is the weighted sum of the prediction of each regression tree. A regression tree is a decision tree that takes in input a feature vector and returns a scalar numerical value in output. At a high level, LambdaMART is an algorithm that uses gradient boosting to directly optimize Learning to Rank specific cost functions such as NDCG.
To understand LambdaMART let’s explore the main two aspects: Lambda and MART. MART LambdaMART is a specific instance of Gradient Boosted Regression Trees, also referred to as Multiple Additive Regression Trees (MART). Gradient Boosting is a technique for forming a model that is a weighted combination of an ensemble of “weak learners”. In our case, each “weak learner” is a decision tree. Lambda At each training point we need to provide a gradient that will allow us to minimize the cost function ( whatever we selected, NDCG for example). To solve the problem LambdaMART uses an idea coming from lambdaRank: at each certain point we calculate a value that acts as the gradient we require, this component will effectively modify the ranking, pushing up or down groups of documents and affecting effectively the rules for the leaf values, which cover the point used to calculate lambda. For additional details these resources has been useful [3] ,[4] . LambdaMART is currently considered one of the most effective model and it has been proved by a number of winning contests.
开源实现:
http://elasticsearch-learning-to-rank.readthedocs.io/en/latest/core-concepts.html
training data & feature vector
- Q = {q(1), q(2), · · · , q(m)} 为训练集中的所有 query
- d(i) = (d(i)1, d(i)2, · · · , d(i)n(i)) 为 q(i) 关联的一组 docs,共 n(i) 个
- x(i)j = Ψ(q(i) , d(i)j ) 是根据 query-document pair (q(i) , d(i)j) 生成的特征向量
- x(i) = (x(i)1, x(i)2, · · · , x(i)n(i))
- y(i) = (y(i)1, y(i)2, · · · , y(i)n(i))
loss function
loss function 用来评估 F(x) 结果的准确性。loss function 用 L(F (x), y) 来表示。 现实世界中,我们可以用 NDCG 来定义损失函数。
formulation of the listwise loss function on the basis of probability models,
title description sciif publishTime 的权重
Learning to rank 存在的问题
长尾
Learning to rank 很大程度上依赖训练数据,而训练数据则来自于真实的用户查询。但是对于长尾查询,统计数据很有限 & 点击行为随机,不具备较好的统计学意义,训练的模型可能并不会起到优化的效果。
传统搜索的质量
如果传统的 BM25 算法由于调参/query 语句不够好,导致排序结果不准确,基于不准确的排序结果产生的用户行为作为训练数据,可能导致训练的模型较差。
这种做法有可能导致 self-reinforcing bias。假如之前的算法给用户优先返回的是关联度一般(mediocre)的内容,用户又基于这些一般的内容产生了大量的点击行为。如果基于这些 click 来 rerank 结果的话,就会产生 self-reinforcing bias,持续推荐 mediocre result.
click 不能准确表示用户意义上的相关度
click 并不能准确表达 content & query 的 relevance, 我们一般用 click & dwell 来确定 content & query 的 relevance
references
When click scoring can hurt search relevance — towards better signals processing in search
Machine Learning for Smarter Search With Elasticsearch Learning to rank
How is search different than other machine learning problems? What is Learning To Rank?
http://blog.csdn.net/starzhou/article/details/52413366
http://alexbenedetti.blogspot.jp/2016/08/solr-is-learning-to-rank-better-part-2.html
https://sourceforge.net/p/lemur/wiki/RankLib/